眼球运动:集合和散开的概念
集合和散开可以简单的理解为眼球的内转和外转。人类在漫长的进化过程中,发展出了完善的眼球运动系统,以达到增大视野,使注视物体落在视网膜中心,以及双眼始终对准目标共同注视,来达到双眼同时单视的目的。正常情况下,眼球的运动均为双眼共同的运动,协调一致,密切协作。
两眼的共同运动形式有同向和异向两种,例如,眼前有汽车从右到左驶过,双眼也会追随汽车从右到左运动,眼轴始终平行,这就是同向运动。而我们视功能上研究的水平聚散运动(集合和散开),是异向运动。聚即为“汇聚”、“集合”、“辐辏”,散即为“发散”、“散开”。
例如,一个笔尖从远到进接近我们,两只眼睛为了能共同注视这支笔,双眼会从平行逐渐内(鼻侧)转,动用集合,做出水平异向运动。这时的运动双眼轴是不平行的,方向相反。若从近到远再把物体移走,就对应双眼向外(颞侧)转的散开运动。
这个从远到近动用集合的过程,也是前面讲到的视近三联动之一。(视功能调节第二篇)
眼用棱镜:构造及光学特性
小学科学课上,老师曾拿三棱镜为我们演示,将太阳光分解为赤橙黄绿青蓝紫的彩虹色。

三棱镜的折射
通过这个图示我们可以发现,光线在进入和射出三棱镜的时候各发生了一次折射,光线的方向发生了改变。眼用棱镜就属于三棱镜的一种,利用的就是它改变光线方向的能力。
概念:
对于眼位异常,视功能障碍者,眼视光学常用三棱镜来检查,训练和矫正,我们称这一类棱镜为眼用棱镜。
眼用棱镜有多种形式,包括搓板形,新月状和楔状,比较常用的是楔状。

题外话:这个搓板形的结构可以让镜片在不增加厚度的情况下正常折射光线,但对入射光线角度有要求,眼用方面其实较少,在海上灯塔上很常见。它其实就是“菲涅尔透镜”。
构造:
由两个平面相交形成的三角形透明体构成,其中两个平面相交的线为棱,习惯称之为“基尖”,与基尖相对的是“基底”。
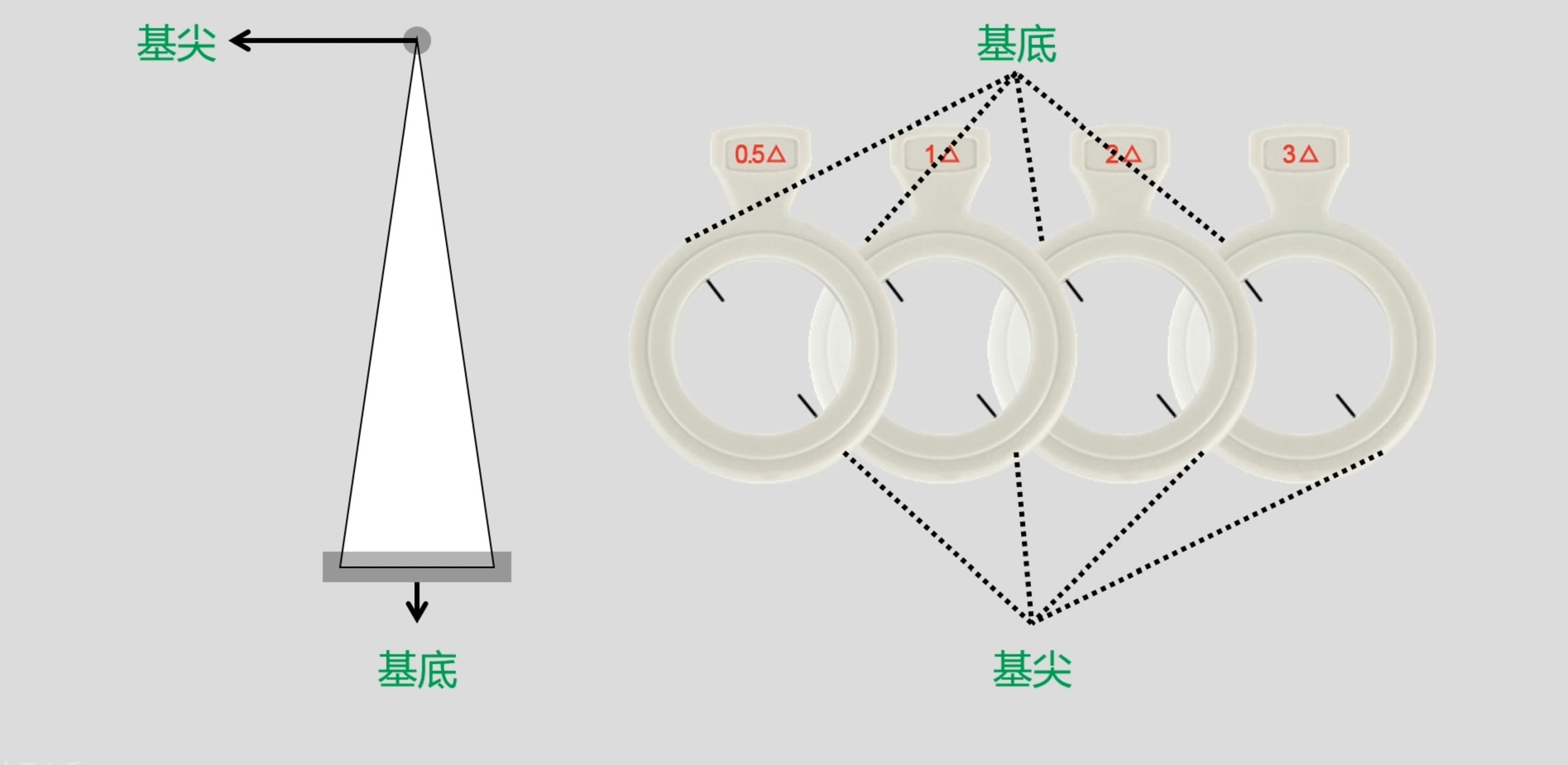
我们验光箱里面的棱镜片就是楔状棱镜,通常靠近手柄的一侧是基底。比较大的棱镜是可以用手感觉到厚度差异的,厚的为基底,薄的为基尖。
光学特性:
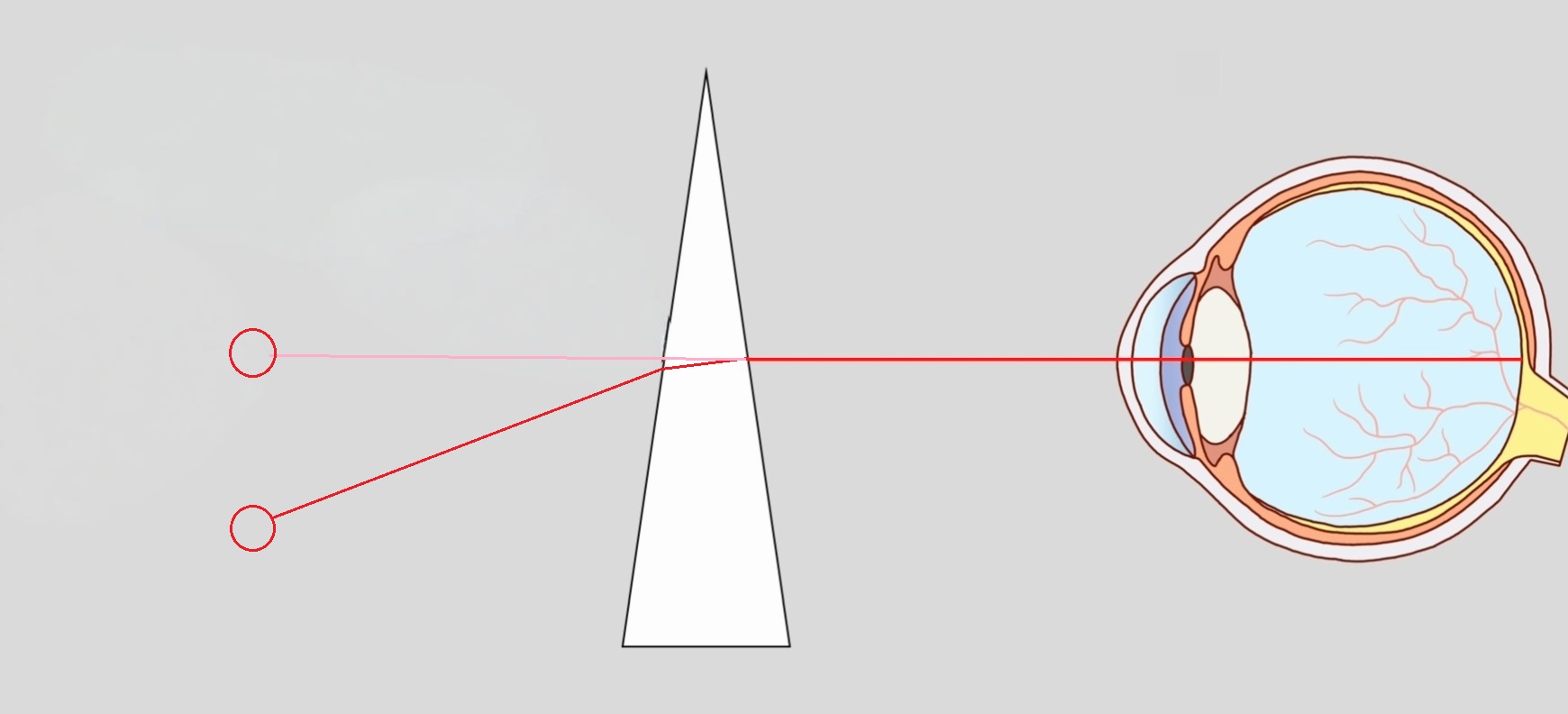
图例中,下方物体发出的光线(深红色)偏移,人眼本能的认为物体在偏上(浅红色)的位置。
当光线通过棱镜后,改变了传播方向,光线向基底的方向偏斜,人观察到的发光点(物象)向基尖方向移位。
棱镜与球镜的关系:
进一步提问:棱镜和球镜都是通过折射光线来起效,那么它们在结构上有有没有相似之处?有的兄弟,有的有的。
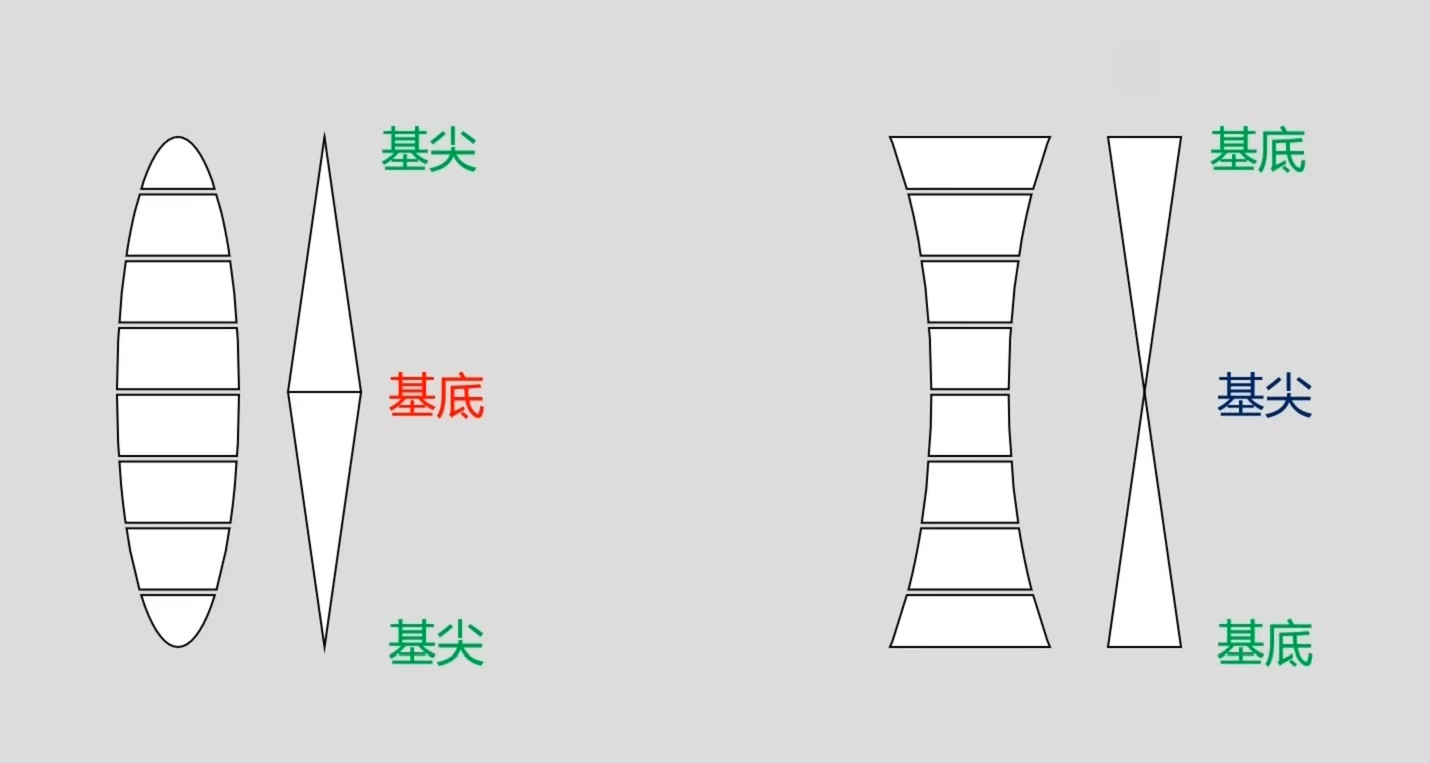
无数基底相对的三棱镜,可以组成正球面透镜,也就是凸透镜。
无数基尖相对的三棱镜,可以组成负球面透镜,也就是凹透镜。
结合这一图解,我们就能理解为很么凸透镜是汇聚光线,凹透镜是发散光线。
理解了这个概念之后,我们就知道为什么在验配中要测量单眼瞳高和单眼瞳距了。就是为了避免眼镜的球面透镜光学中心点偏移,导致视轴与光学中心移位,产生类似于用棱镜视物的效果,也就是我们常说的棱镜效应。由于再完美的装配也不能确保每次配镜都相同且精确,我们常说的新镜需要适应一下,有一部分原因就是因为新旧眼镜棱镜效应的些微改变。
注:这个光学中心偏移量的误差国家是有标准的,合格的验配不会影响视觉健康。不在行业内的小白读者不必因为这些专业数据而焦虑。实际上,由于眼球的转动,你的瞳孔并不总是对准光学中心;并且,在给加工师傅提供参数时,验光师可能会考虑使用者的用眼习惯而主动做出一些偏移,比如一些专业台球运动员(他们总是用镜片的上半部分)的工作镜需要偏上一些,看手机电脑多的人(近用场景往往发生在镜片下半部分)会适当偏下一些。
棱镜度:集合的常用表述方法
集合以棱镜度(△)来表示,1△即为光线通过1m远的距离,产生1cm的垂直偏离。
例如,当人眼观察1m的物体,加棱镜后物体偏移了1cm,那么这个棱镜就是1△。
计算公式:双眼集合需求(△)=瞳距(cm)÷注释距离(m)
举例说明:
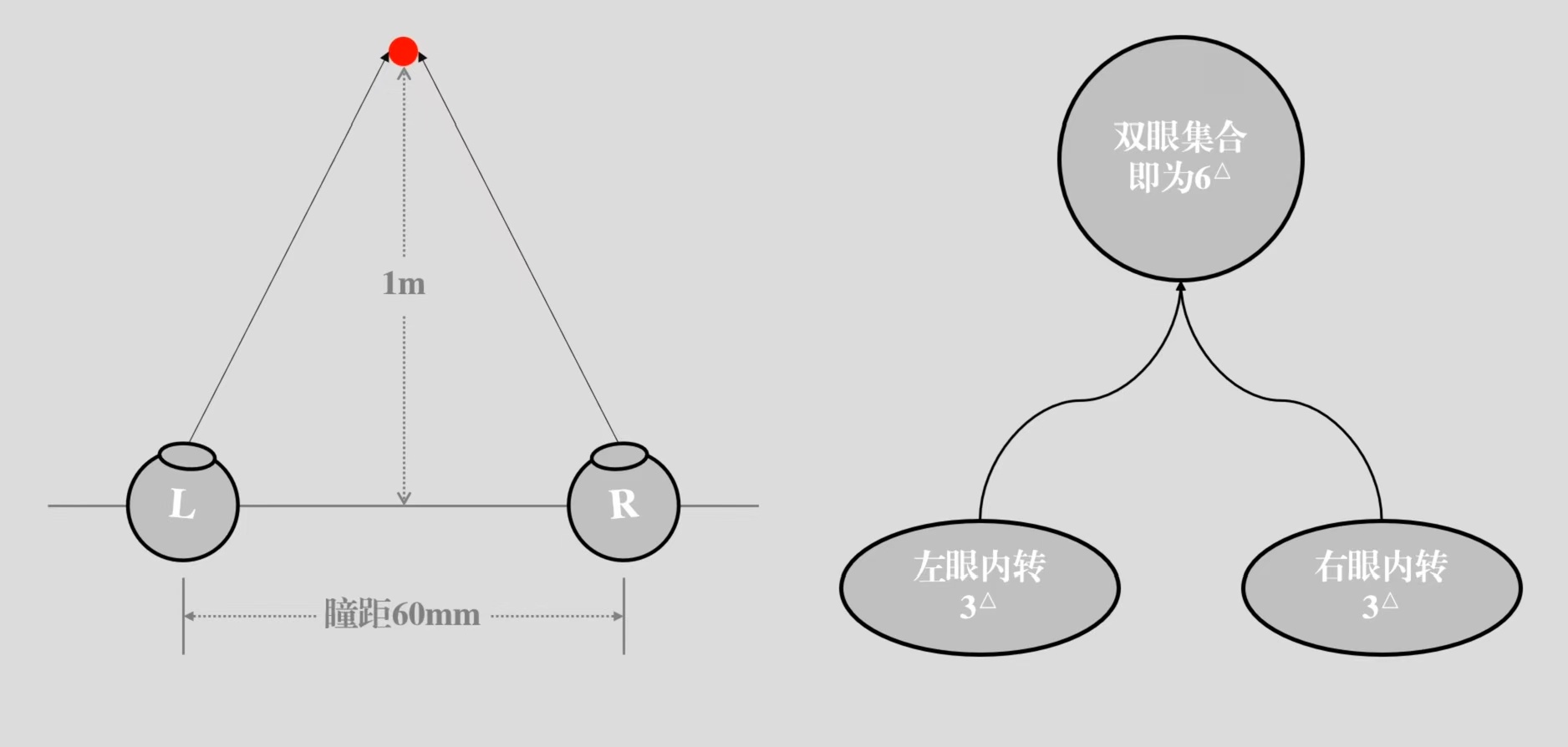
假设瞳距为60mm的人眼在观察自己正前方1m的物体,此时在水平方向上两只眼睛各需要在1m的距离上做出3cm的内转,两只眼睛总共动用6cm内转,此时两只眼睛各转动了3△,双眼集合为6△。
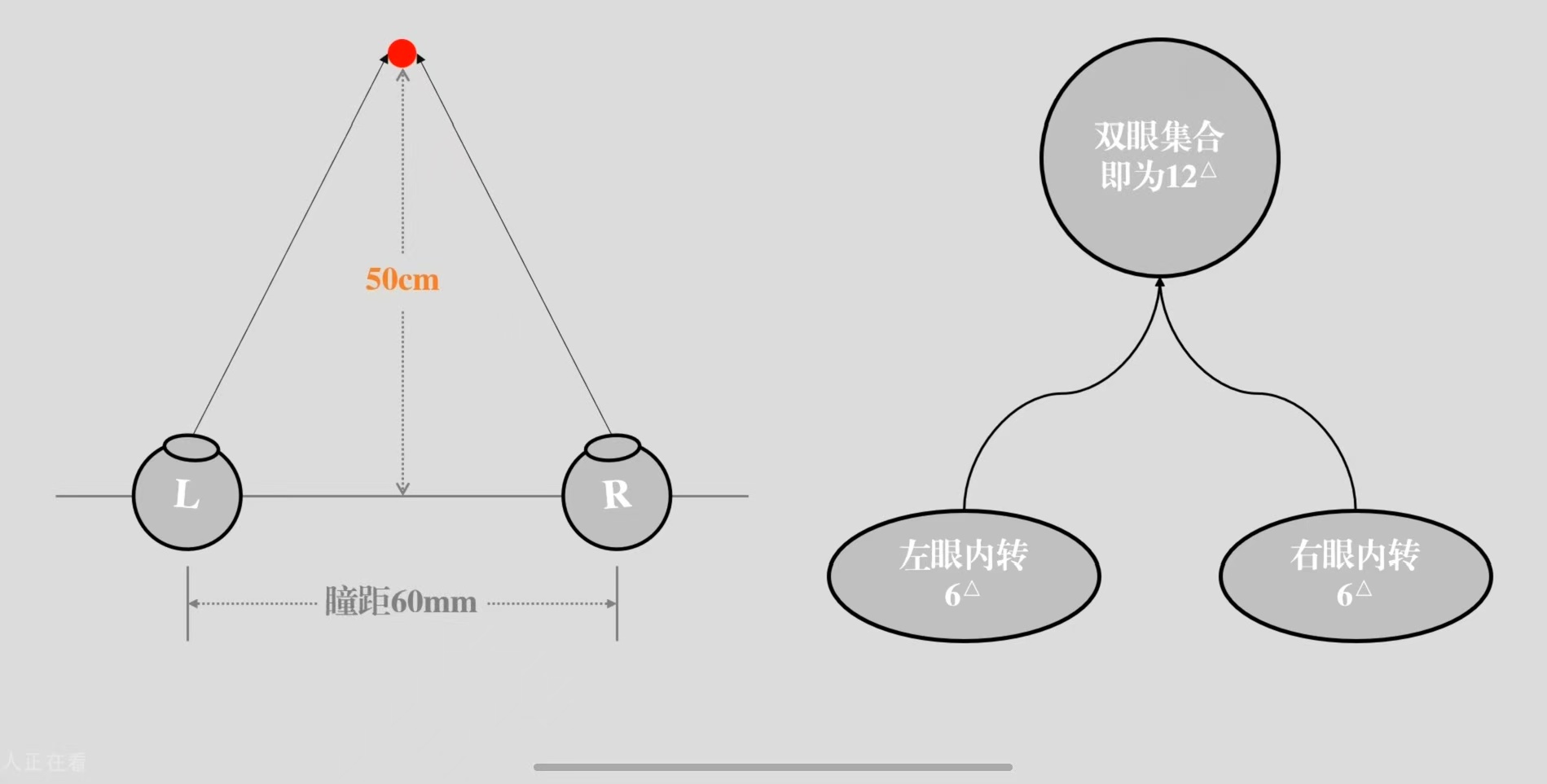
假设这个物体移近了50cm,此时人眼所需动用的集合翻倍,单眼各动用6△,双眼12△。
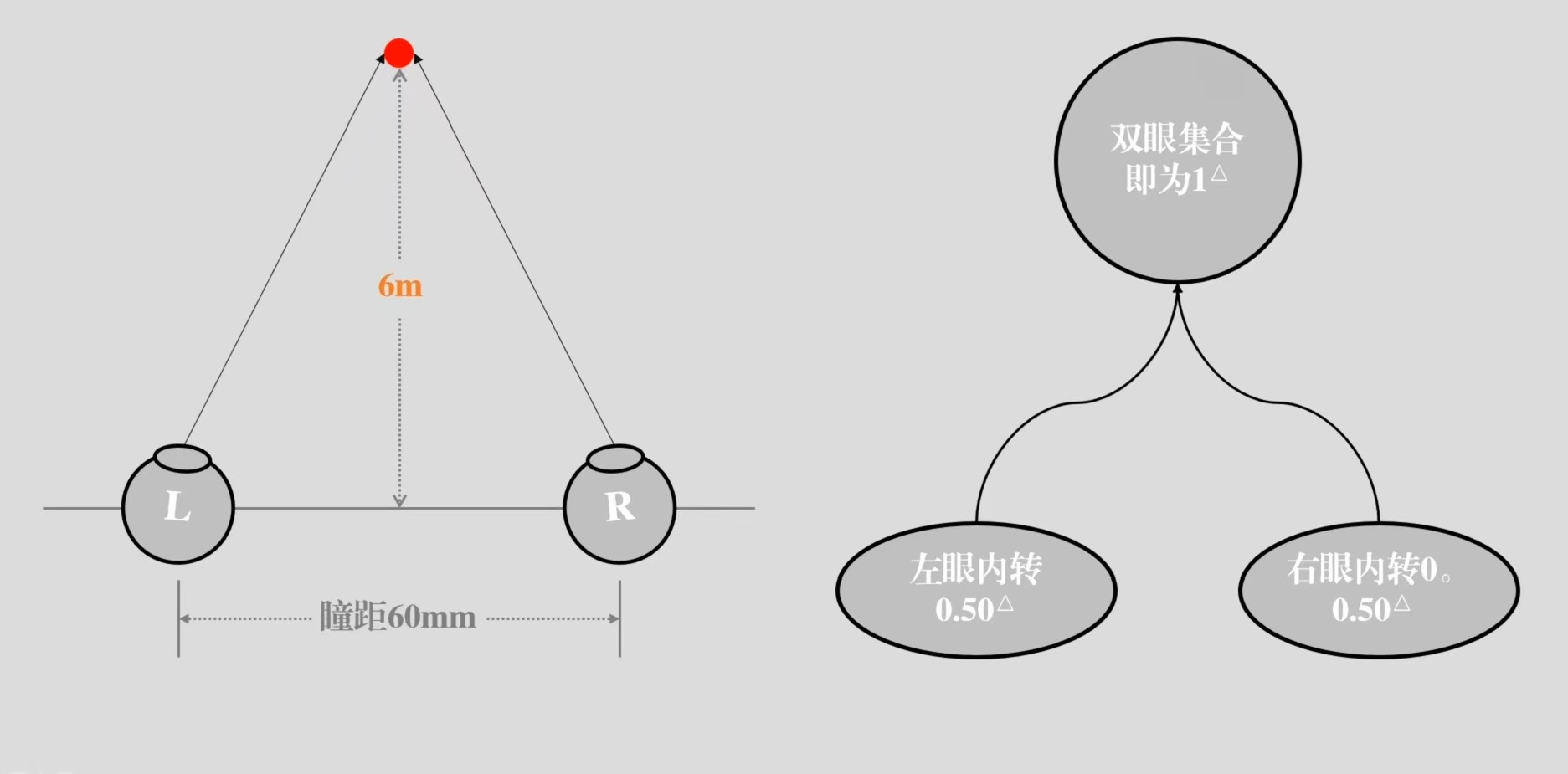
假设这个物体移动到了6m,此时人眼每只眼仅需0.5△,双眼为1△。
米角:集合的另一种表述方法
1米角(MA)表示双眼注视眼前1米处物体时的集合量,每只眼的集合量为总量的一半。其数值为“位于双眼中点平面与双眼旋转中心的连线中央的距离的倒数”(什么寄吧玩意,看不懂)
大白话:注视距离的倒数
举例说明:
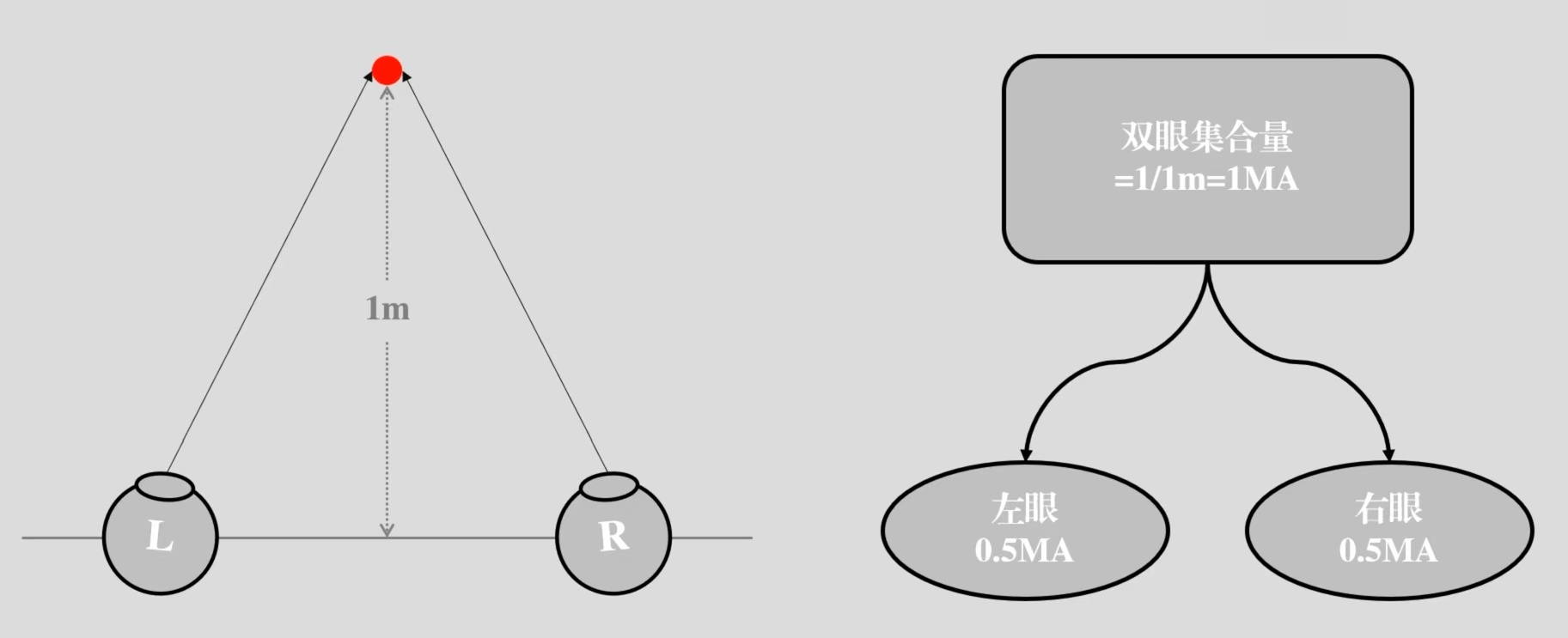
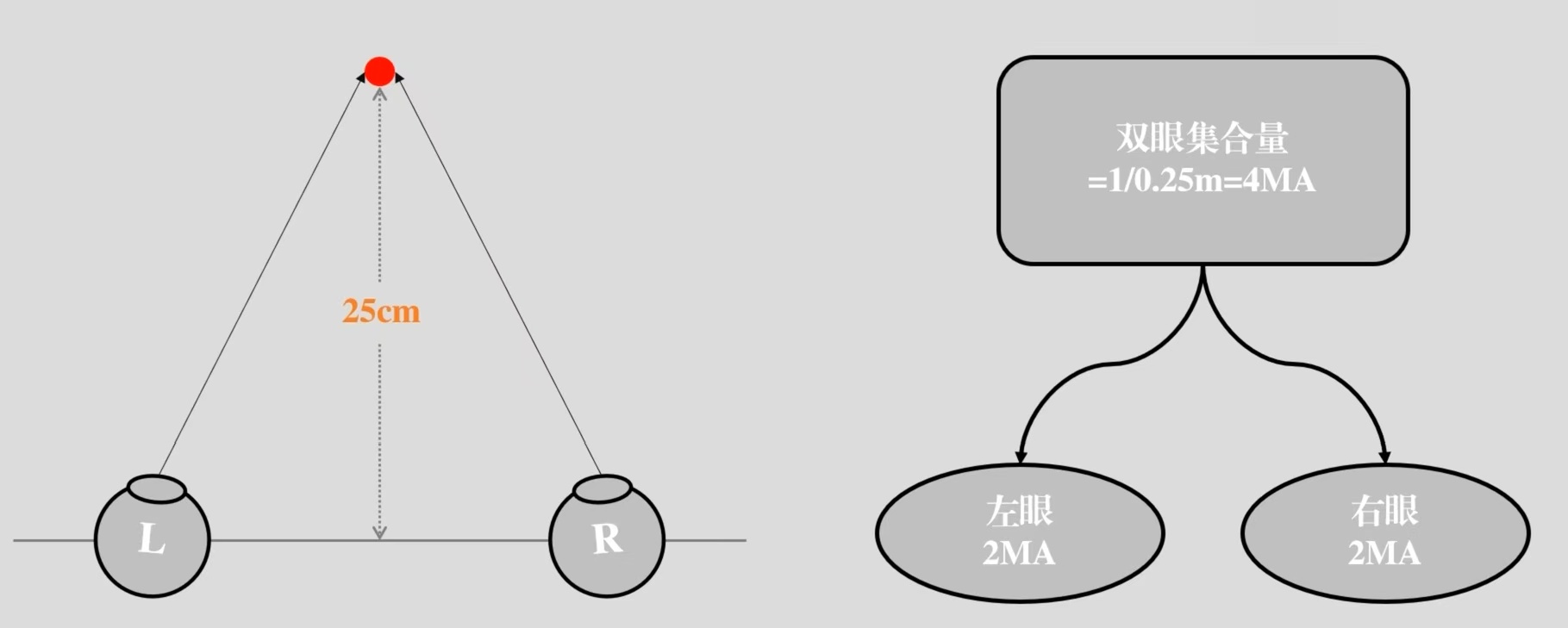
我们可以发现,米角的计算公式不考虑瞳距,它只是一个相对单位,只与距离唯一相关。对于不同瞳距的人,相同的距离计算出来米角视相同的。它的计算方法有点类似于所需调节的计算。
