这章重点记录如何区分单纯性散光,复性散光和混合散光。基础的类别定义详见第一章。
先明确一点:
①球柱镜的正负散表达式,就是分别将两条子午线的其中一条作为球镜基础,将两条子午线之间的差值作为附加球镜来表达。
②单纯凭借等效球镜来判断散光类型是不准确的(详情见下方的蓝色结论)。
⚪单纯近视性散光:一条子午线位于视网膜上,另一条位于视网膜前。
⚪单纯性远视散光:一条子午线位于视网膜上,另一条位于视网膜后。
单纯性散光有一条子午线在视网膜上,因此我们一定可以在表达式上把球镜度数换算为零。此时,柱镜的符号就决定了单纯性散光的近视和远视。
例:
-1.00DS/+1.00DC*180经过换算后可得:0.00DS/-1.00DC*90,这个散光是单纯近视性散光。
+1.00DS/-1.00DC*180经过换算后可得:0.00DS/+1.00DC*90,这个散光是单纯远视性散光。
总结:球镜为0,或者球柱镜度数相等符号相反的,为单纯性散光。将球镜换算为0后,柱镜的符号就决定了它是近视性还是远视性。
⚪复性近视散光:两条子午线都位于视网膜前。
⚪复性远视散光:两条子午线都位于视网膜后。
复性散光两个子午线都同时位于视网膜的一侧,因此一定可以书写成“负球镜+负柱镜”或者“正球镜+正柱镜”的形式。此时,球柱镜的符号就决定了它是复性近视散光还是复性远视散光。
例:
-1.00DS/+0.50DC*180经过换算后可得:-0.50DS/-0.50DC*90,这个散光是复性近视散光。
+2.00DS/-1.50DC*180经过换算后可得:+0.50DS/+1.50DC*90,这个散光是复性远视散光。
总结:若球柱镜符号相同,或球柱镜符号不同但球镜度数大于柱镜度数,这个散光是复性散光。球镜的符号决定近视性和远视性。
⚪混合性散光:两条子午线一条在前一条在后。
混合性散光的两条子午线在视网膜一前一后,我们以其中一个子午线的位置作为球镜基准,那么剩下那条子午线决定的柱镜必定符号相反(位于视网膜另一侧)且度数大于球镜。因此一定可以书写成“负球镜+更大的正柱镜”或“正球镜+更大的负柱镜”形式。
例:
-0.75DS/+2.00DC*180,这个散光是混合性散光,等效球镜为正。
+1.00DS/-2.00DC*90,这个散光是混合性散光,等效球镜为负。
总结:当球柱镜符号相反,且柱镜大于球镜,那么散光为混合性散光,等效球镜的符号与柱镜符号相同。
注意:复性远视散光的等效球镜必为远视,复性近视散光的等效球镜必为近视,但等效球镜不管是近视还是远视,都有可能对应着混合性散光。若等效球镜为0,那么必为混合性散光
注:光学十字线可以准确直观的判断散光类型。
若两条经线其中一条为0,说明是单纯性散光。
若两条经线均为负,说明是复性近视散光;
若两条经线均为正,说明是复性远视散光;
若两条经线一正一负,说明是混合性散光。
以下是几个案例:
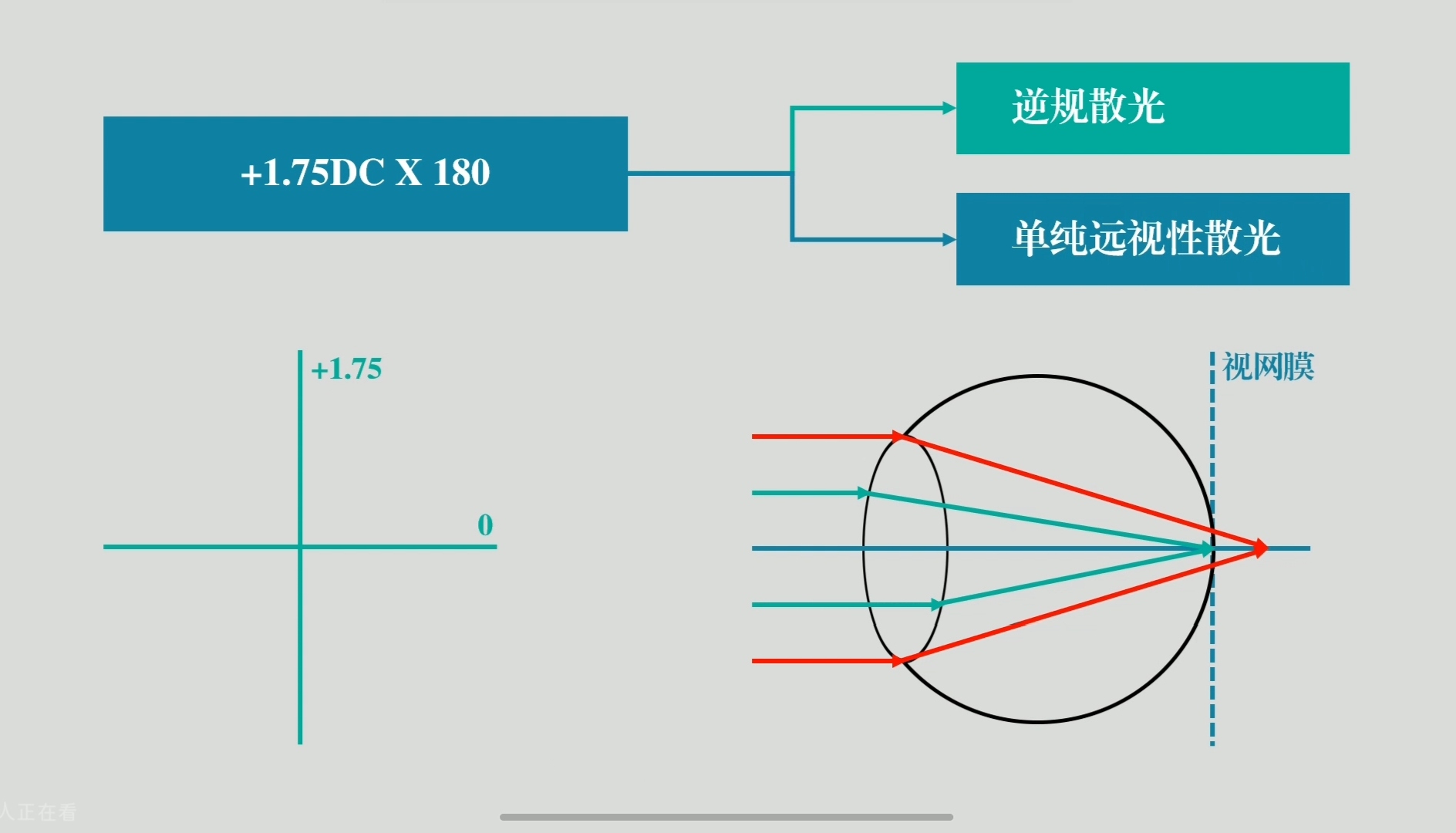
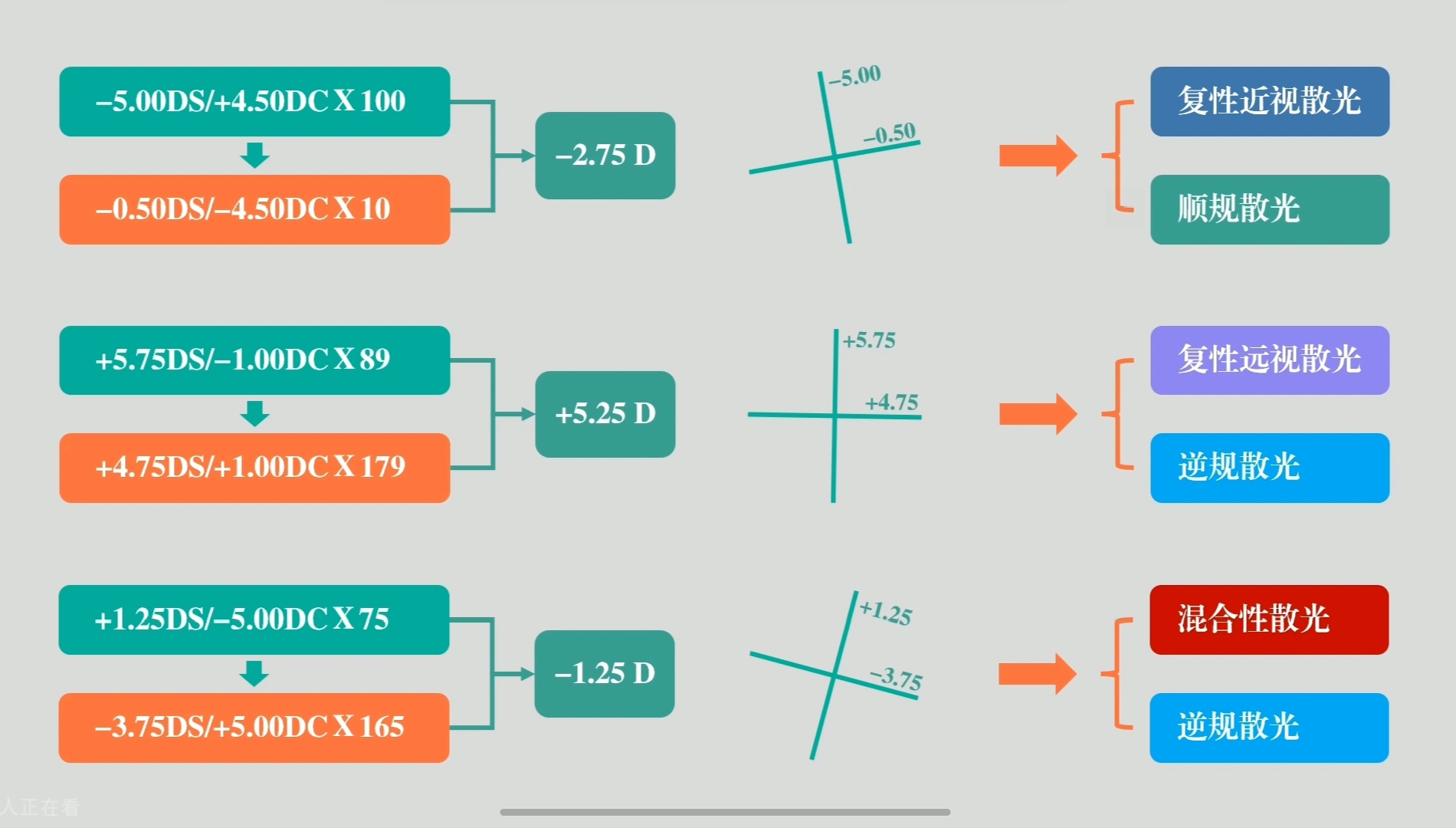
如何区分顺规、逆规散光?
①顺规散光(横轴散光)
两条径线分别位于垂直和水平方向(±30°),且垂直径线屈光力大于水平主径线。正常的角膜形态即是垂直方向屈光力大于水平方向,因此称为顺规散光。
(也就是负散轴位在水平方向的散光)
②逆规散光(竖轴散光)
两条径线分别位于垂直和水平方向(±30°),且垂直径线屈光力小于水平主径线。正常的角膜形态应是垂直方向屈光力大于水平方向,因此称为逆规散光。
(也就是正散轴位在水平方向的散光)
所以,在明白区分原理后,只需要看散光的符号和轴位即可判断。
以负散为例:轴位0-30为顺规,30-60为斜轴,60-120为逆规,120-150为斜轴,150-180为顺规。
