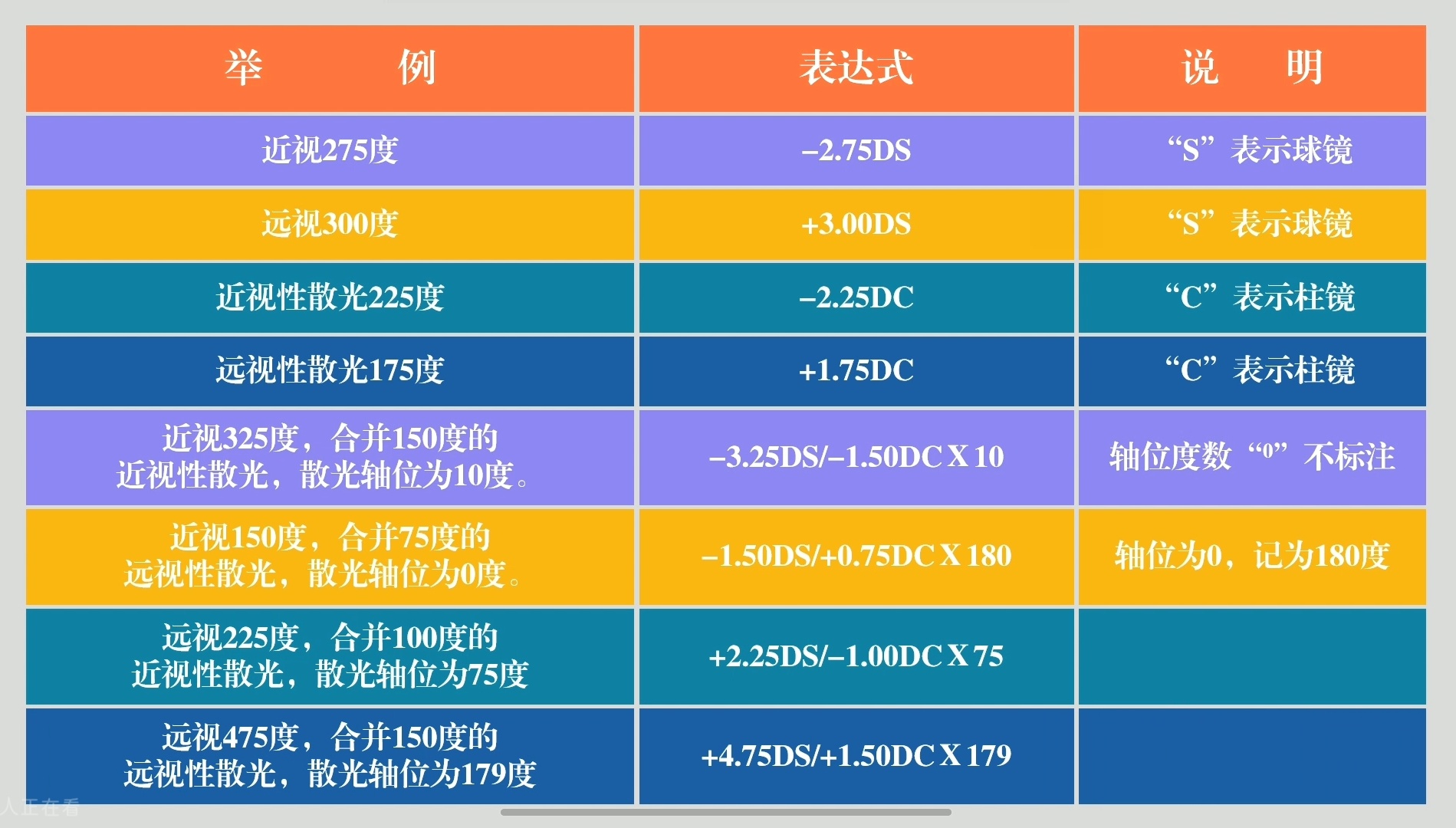
球柱面透镜的表达式
这其中,视光行业最常用的就是负散表达式。也就是把散光写成负镜的形式。
例:-1.00/-0.50×180,可以理解为:在一个-1.00D的球镜(DS)上,额外增加-0.50×180柱镜(DC)。
大白话讲就是:把一个100度近视镜片的垂直方向上额外加50度。此时垂直方向是150度近视,水平还是100度近视。
我们分别记录:基础的近视(球镜)度数、额外的散光(柱镜)度数、这个额外度数的方向(轴位),并按照以上的格式写出来,就得到了这个镜片的表达式。
表达式的正负散换算
很多眼科医生喜欢用正散表达式,是工作中很常见的处方形式。如何换算?
第一步:调轴
把原柱镜轴向旋转90°得到新的轴位,新老轴位相互垂直(超过90的减90,没超的加90即可)。
第二步:换号
散光的数值不变,直接把正负号更换一下写到新的式子。
第三步:代数和
将原球镜度数(带符号)和原柱镜度数(带符号)相加求代数和作为新的球镜度数。
注意:带!!符!!号!!
例:
-2.50/+0.50*70与-2.00/-0.50*160等效
+1.50/+0.75*100与+2.25/-0.75*10等效
光学十字线表示法
顾名思义,该表示法就是画一个十字来代表球柱镜的两条子午线,并标注各条子午线屈光力。
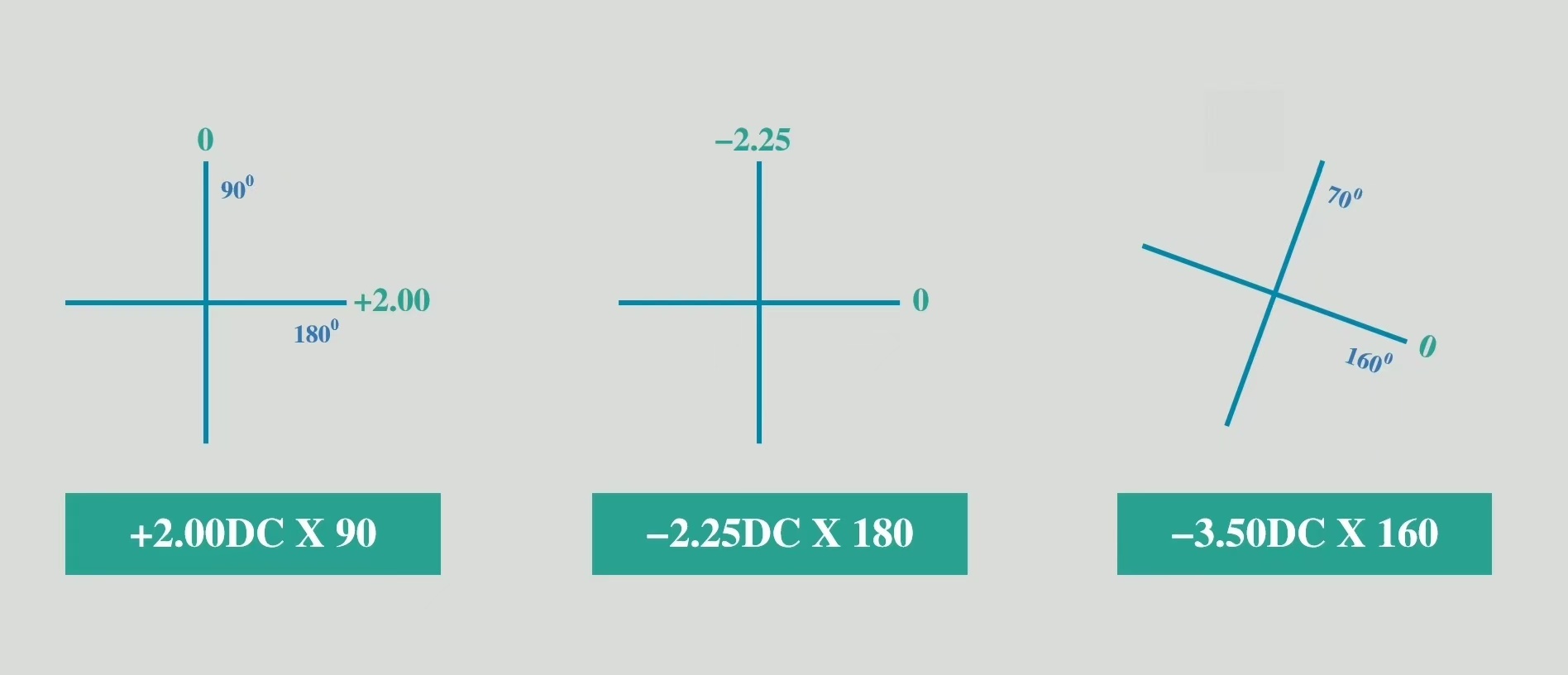
以上是三个单纯性散光的表达式
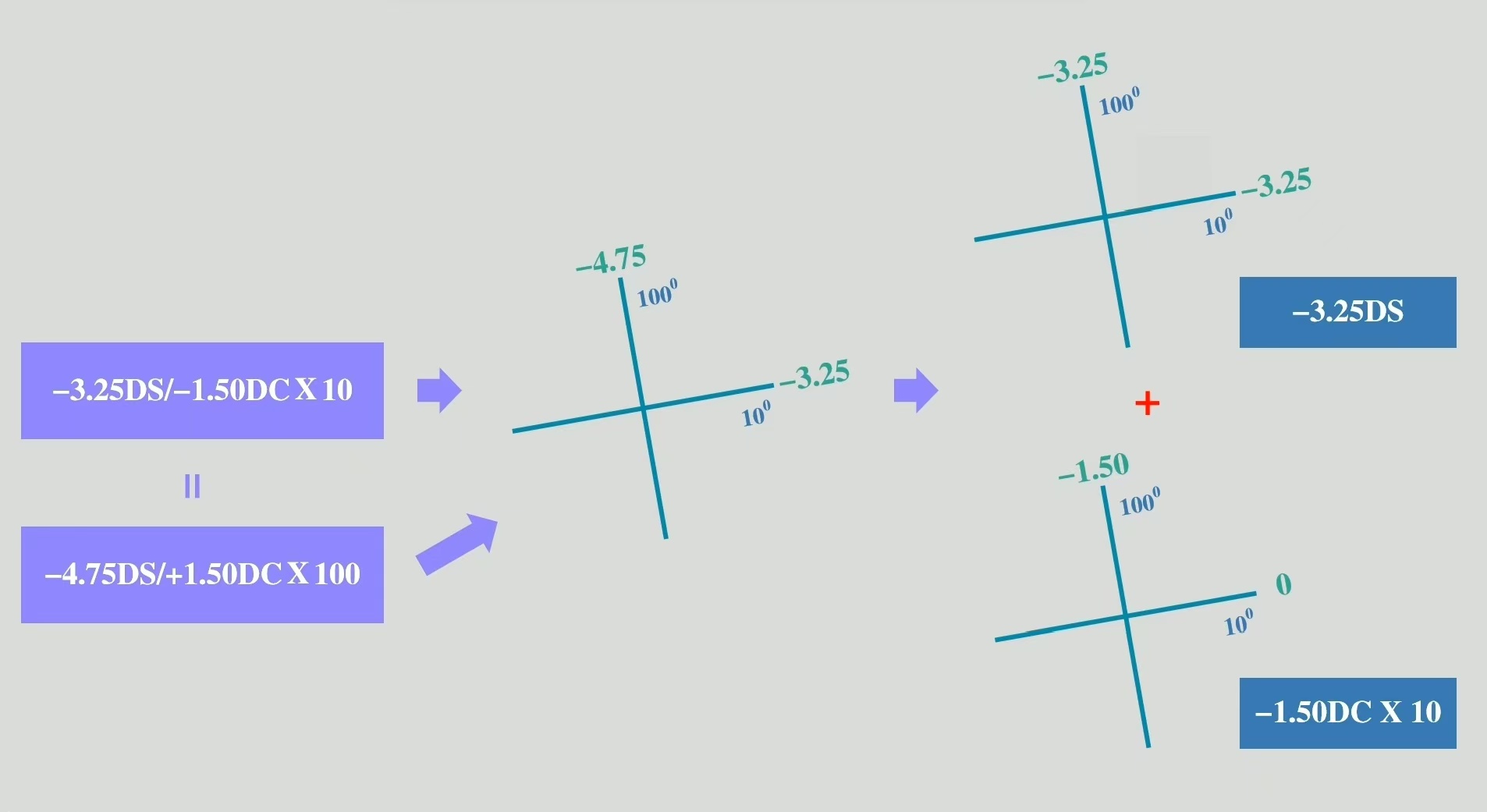
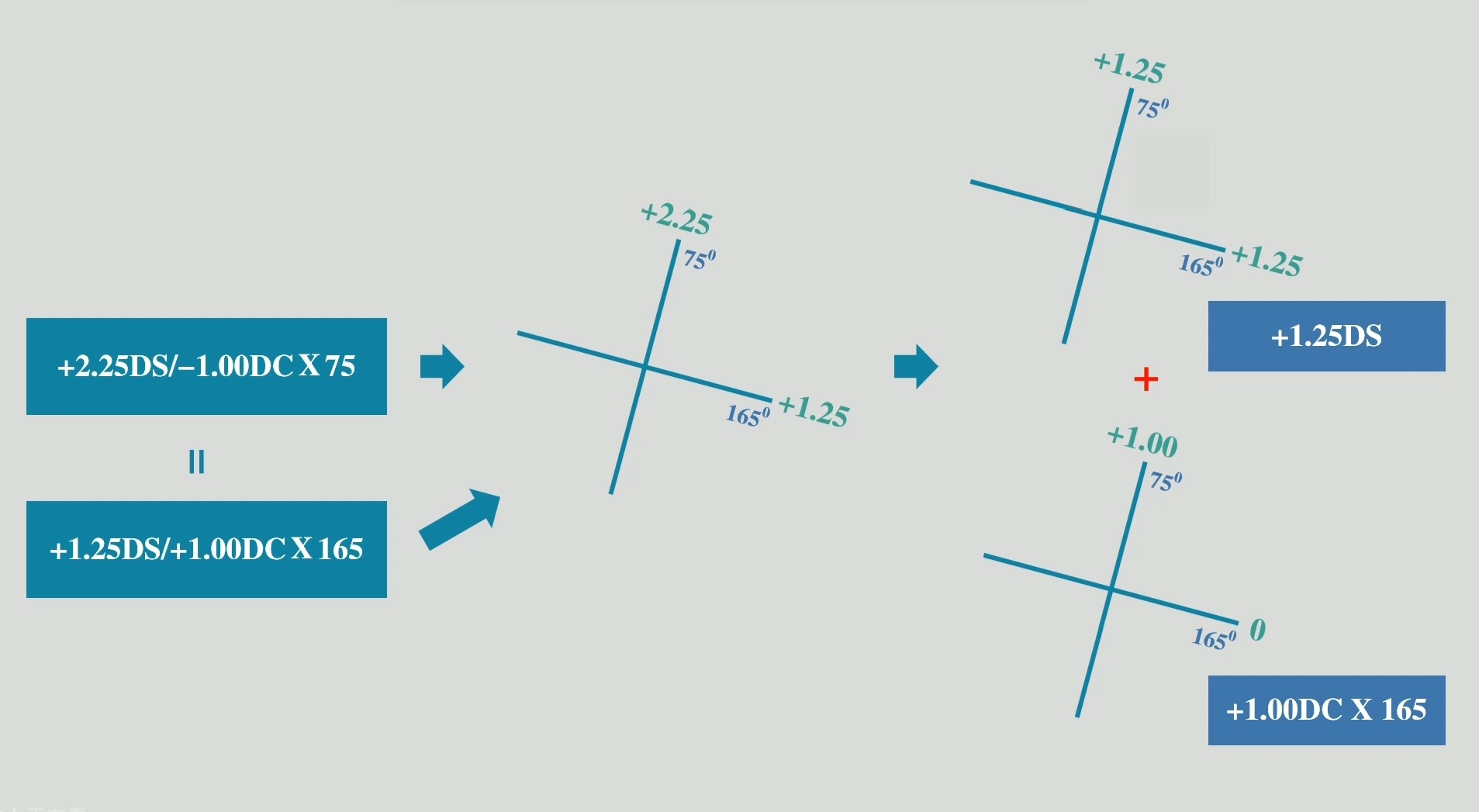
例:以上两个球柱联合表达可以看作一个球镜十字和一个柱镜十字的联合。
以上三个式子:正散表达,负散表达,光学十字表达,也即最常见三种表达方式。
等效球镜的概念和计算
概念:散光透镜的两条主子午线方向的屈光力(也即镜片最大屈光力和最小屈光力)的平均值,就是此透镜的等效球镜度,可以理解为此透镜的平均屈光度。
等效球镜度是负值时,说明最小弥散圈在视网膜前,是近视性的。
等效球镜度是正值时,说明最小弥散圈在视网膜后,是远视性的。
等效球镜的计算:
方法一:球镜(近视)度数+柱镜(散光)度数的一半,即:
等效球镜=DS+DC/2
方法二:将光学十字标注法中的两条子午线屈光度取平均值。这个方法在展示”等效“二字上更直观,但要求熟练掌握十字标注法。
这两种方法本质上是相同的。
例一:-0.50DS/-4.50DC×10
等效球镜为:-0.50+-4.50÷2=-2.75
例二:-5.00DS/+4.50DC×100
等效球镜为:-5.00+4.50÷2=-2.75
再次提示:
等效球镜对应着上一章的”最小弥散圈“的位置,但由于这个地方依然是最小弥散“圈”,所以等效球镜≠等效物象。所以散光在能适应的情况下老老实实验配,该加就加,视觉效果更有保证。
等效球镜的计算在高散光初次配镜不适,或者隐形验配中比较常用。