通过视功能调节篇，集合篇，以及调节与集合的关系的笔记，我们大体了解了调节与集合的概念，它们是如何工作的，以及它们之间联动的大致关系。但说到调节与集合的关系，除了上一篇所讲的基础知识，还有一个重要的概念：AC/A。

AC/A的概念

这是一个极其重要并且极其具备实践意义的概念，也就是“调节性集合与调节的比值”

人眼看远处时，调节和集合都处于放松状态，为0。而人眼在看近时，调节和集合联动发力，维持清晰物像和双眼单视。不同的人或同一个人在不同状态下，动用同样的调节时带动的集合是不同的，衡量这个“带动能力”的指标就是AC/A。AC/A的正常值是3-5

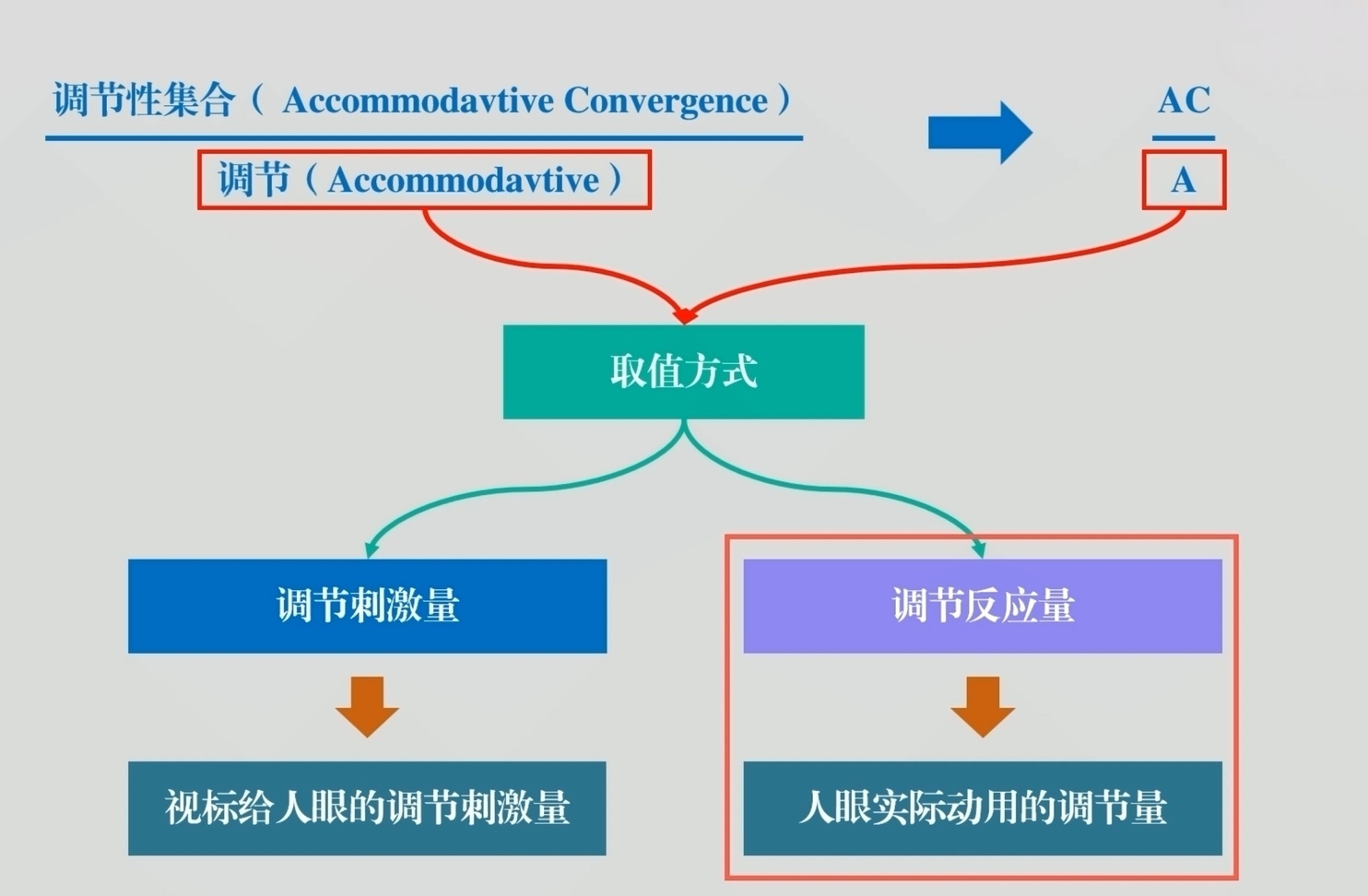
这个“A”也就是调节，有两种取值方式：一种是取调节刺激的量，一种是取调节反应的量。

我们要知道，大部分人眼是略微调节滞后的，也就是调节反应小于调节刺激，所以当我们用实际的调节反应的量来取值时，分母小，取值就会大。显然，用实际的调节反应的量来取值测量AC/A，要更精准。

但是，实际的调节反应的量的准确值，需要用到动态视网膜检影的方法，工作量较大。因此实际中，我们一般还是使用调节刺激的量来计算AC/A。其实只要严格按照视功能检查流程和要求来，两者的值不会有明显区别。

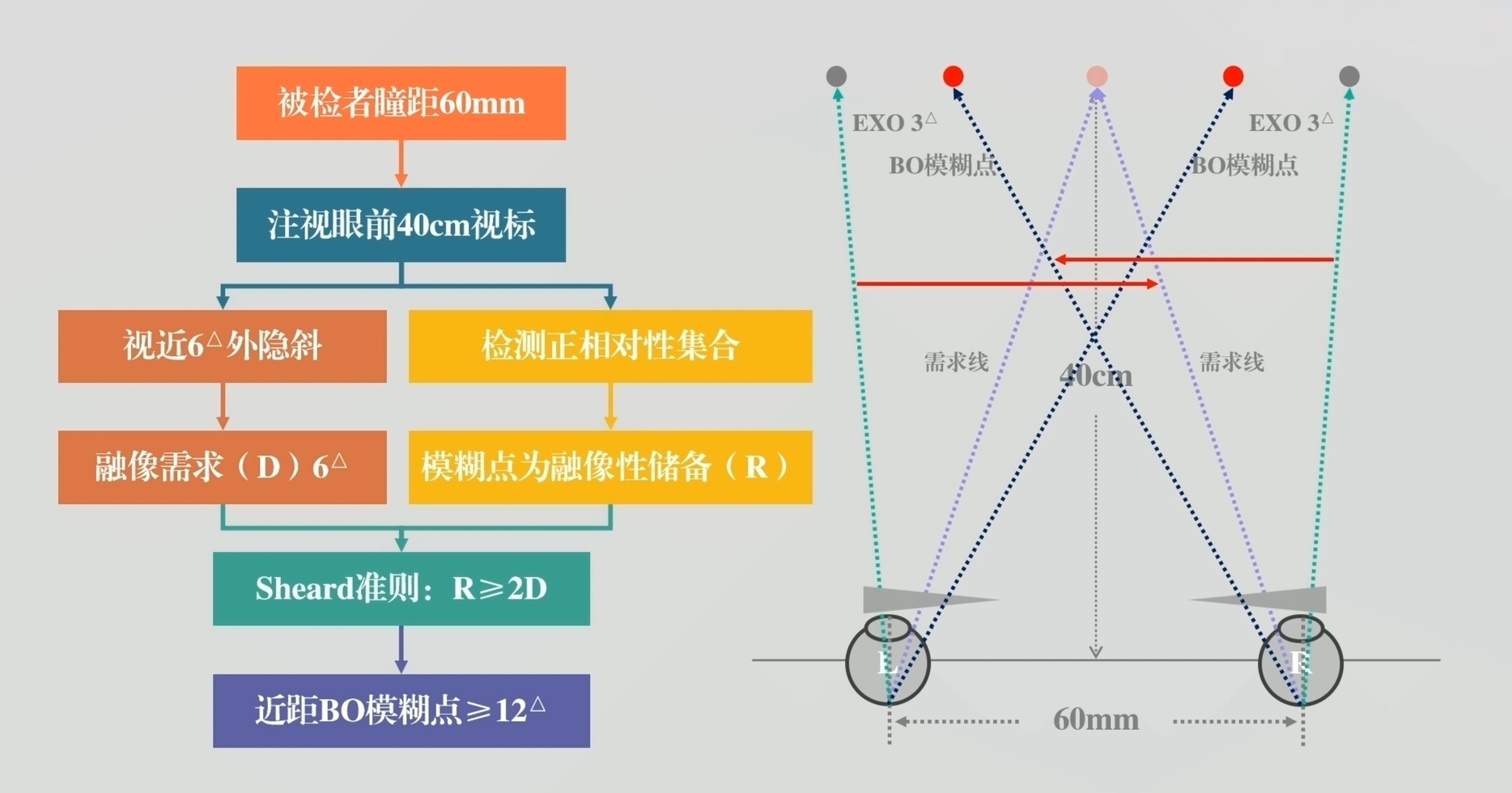
我们假设一个人瞳距60mm，远近均无隐斜，观察40cm视标，在理想状态下看他的AC/A:

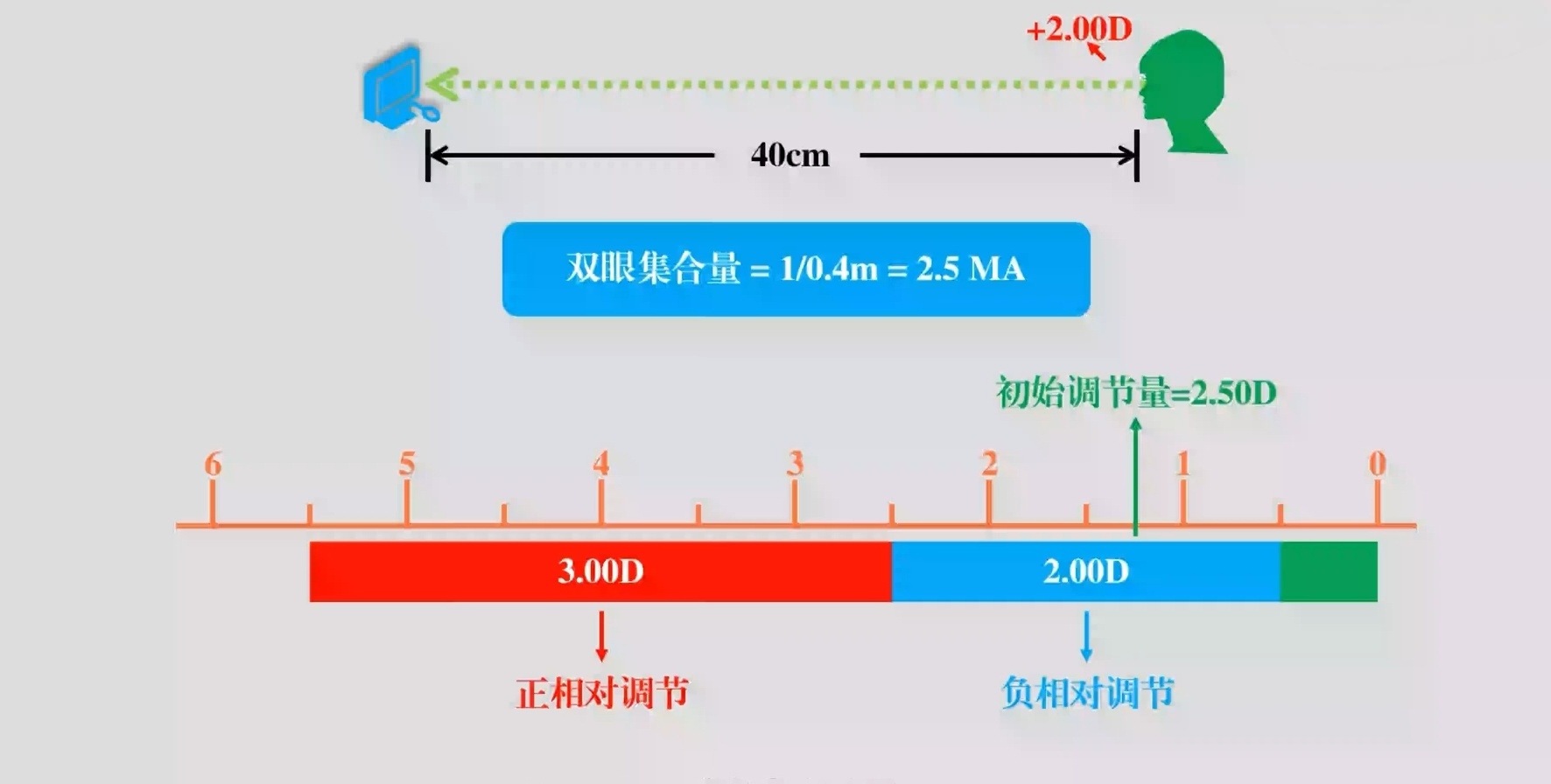
调节刺激：1/0.4m=2.50D

集合刺激：6cm/0.4m=15△

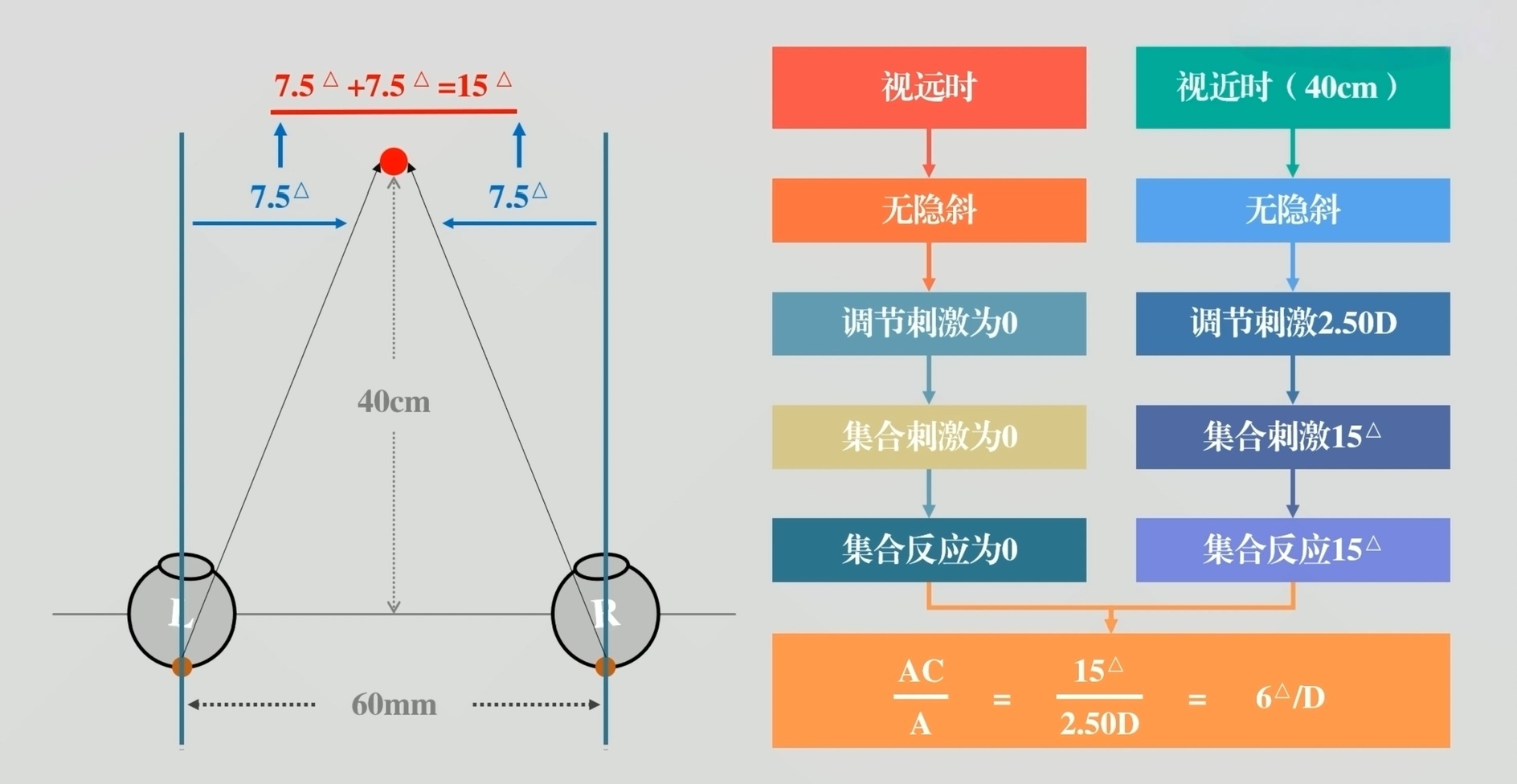
此时，他动用了2.5D调节，这2.5D调节带动了15△集合，他的AC/A就是15△/2.5D=6，也就是“每动用1D的调节，带动6△的集合”。

需要注意，这个例子完全没有考虑隐斜，而完全没有隐斜的人极少极少，因此计算AC/A时看远看近的隐斜时必须要考虑的。

AC/A的计算

例1：

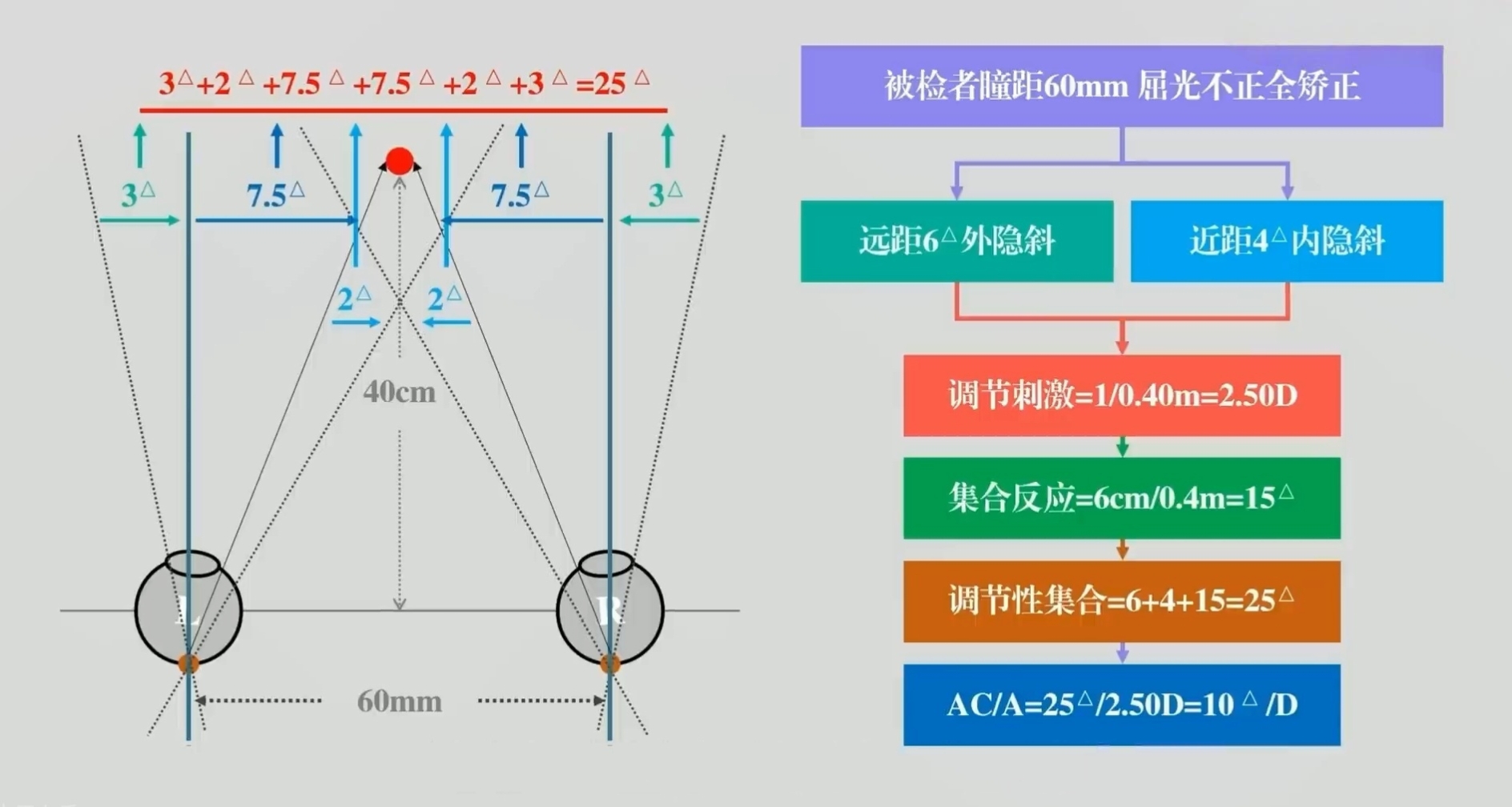
假设被检者瞳距60mm，屈光全矫，远距隐斜为6△BI，近距隐斜为4△BO，注视40cm视标。

这时，被检者的调节为2.50D，眼位要到达内隐斜位置，则需要在固定的15△集合反应上再多克服远距的“更远”的外隐斜和加上近距的内隐斜，也就是15△+6△+4△一共25△。所以，被检者的AC/A应该是25△/2.50D=10。也就是说，他每动用1D调节，则可以联动10△的集合运动。

例2：

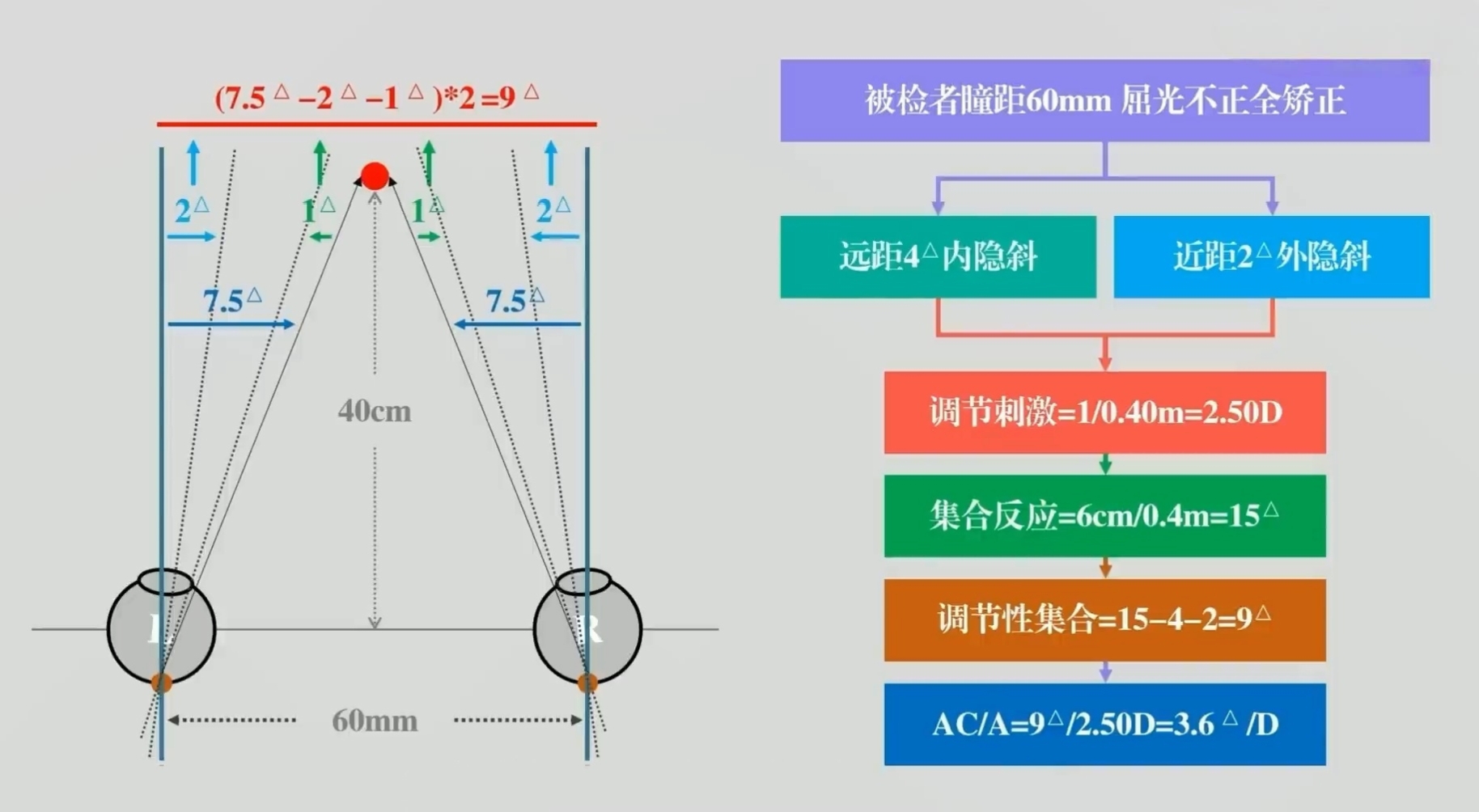
假设被检者瞳距60mm，屈光全矫，远距隐斜为4△BO，近距隐斜为2△BI，注视40cm视标。

这时，被检者的调节为2.50D，眼位要到达内隐斜位置，则仅需在固定的15△上减去“更近”的远距内隐斜和减去近距外隐斜，也就是15△-4△-2△=9△，他的AC/A应为9△/2.5D=3.6。也就是说，他每动用1D调节，则可以联动3.6△的集合运动。

我们将以上作图计算，其内隐斜计为正，外隐斜计为负，省略到数学换算和简化，可得公式：

AC/A=瞳距（cm）+（近距隐斜-远距隐斜）/2.50

AC/A的意义与应用

之前说过AC/A是极其重要并且极其具备实践意义的，具体可以表现在如下几个方面：

①参考判断调节性内斜视的类型：

调节性内斜视可以分为两种，一种是屈光性调节性内斜视，这种内斜视是由未经矫正的远视度数引起的，在中高度远视的儿童身上常见，它的AC/A是正常或接近正常的。所以，在佩戴准确度数的矫正眼镜后，内斜视会消失。

另一种是非屈光性调节性内斜视，它也可能伴随一定的远视度数，但斜视原因与远视无关，它表现为AC/A的值很高，过高的AC/A引起了过高的集合，导致内斜视。

通过对比AC/A的值，就可以参考判断调节性内斜视的类型。在实际工作中，还需要结合其他指标综合判断。

②为配镜处方提供参考：

对于近视远视是否应该及时配镜，有参考意义。

a.针对近视：

很多孩子近视以后因为父母的固执己见，或者自己觉得不方便，不美观，不愿意戴镜矫正，此时检查时我们会发现，其在看近时有外隐斜，并且AC/A偏低。那么我们可以基本判断其外隐斜有发展为外斜的可能性。

b.针对远视：

也是由于很多孩子不戴镜，检查时若发现在看近时有内隐斜，并且AC/A值偏高，那么我们可以基本判断其内隐斜有发展为内斜的可能性。

c.针对低AC/A的人群，由于其调节联动的集合量比较少，所以改变配镜处方对隐斜的影响也较小；相反，针对高AC/A的人群，因为调节联动的的集合大，那么改变处方对隐斜影响也大。

③参考分析视功能异常：

视功能分析当中，AC/A是一项重要的指标。在后面的笔记会有。

高AC/A一般对应的是“集合过度”和“散开过度”，低AC/A一般对应的是“集合不足”或“散开不足”。